Here, it’s the slanty side, labeled “c.” In Right Triangle Land, the hypotenuse is always “c.”
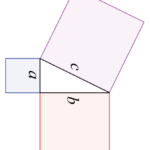
I don’t know if it happened in some regular math class, or in Algebra or in Geometry, or in all of them, but at some point I learned the term “hypotenuse” and what it meant–which is: In a Right Triangle (which is any triangle that has a right angle [90°]), the side opposite that right angle is called the hypotenuse. And I find the idea useful when I’m walking in parking lots.
When I’m shopping, let’s say at Target, and I leave the store with my bag(s) and maybe a cart, I’ve got to walk across two lanes of parking lot traffic to get to the parked cars. The drivers in those lanes are, of course, or at least we hope of course, driving pretty slowly. One: they’re trying to be careful of pedestrians entering and leaving the store. Two: they’re trying to find good parking spots. Hmm. I think finding the parking spots might be their first priority, and the shopping public a little further down their list of concerns. But, ordinarily, no one is speeding in that space in front of the store’s entrances. (And, there are a couple of stop signs, too.)
When shoppers leave the store, they usually head precisely toward the spaces where their cars are parked, because the shortest distance between two points is a straight line (also a Geometry fact).
Let’s say that some guy parked his white car in the spot that’s way over on the left side of the photo. He may have parked there because he’s got to return something, and the Customer Service counter is by that closest door, the one at the front of the right-hand side on the photo. He returns his merchandise and then thinks that he might like to have a latte from the Target Starbuck’s, so he walks on down there. Then, he thinks he’s hungry, too, and a pretzel would be tasty. The snack bar is right beside the farther door, so he gets his pretzel and walks out that door. Then, he realizes that he’s gone out the wrong door, but it’s early in the morning and not blazing hot, yet. So he starts walking toward his car. He walks in a straight line (that being the shortest distance), from the door to his car, i.e. diagonally across the whole length of those lanes. And, if I and someone else are driving up towards him, and a couple of other cars are approaching from behind him, we’ve all got to stop and wait for him to make that long walk. We might be able to inch up some, but basically, at some point, his walking is slowing down both lanes of car traffic. Instead, the more helpful route would have been to leave the building and walk straight across that lane where cars drive (see Side a, above). Then, he could walk down Side b, towards his parked car, still having to cross the distance between the lines of parked cars where vehicles might be driving, but there wouldn’t be quite as much traffic slow-down. Or, he could have walked all the way down the sidewalk in front of the building (side b) and then across the busier lanes (side a). And, obviously, at 8:30 in the morning (photo time), it’s not much of an issue. But, on a Saturday afternoon. Ollie, Mollie, Gollie. It really would help a lot!
Same thing at the HEB grocery store. There is a much wider space for cars driving back and forth, coming and going, searching for the best place to park. But the grocery store shoppers often have filled-to-the-brim carts and sometimes lots of family members, some of them rather short. Walking straight across instead of opting for the lengthier, diagonal route, would be safer.
In Math Classdom, the hypotenuse is famous for its place in the Pythagorean theorem, which Wikipedia defines as:
In mathematics, the Pythagorean theorem, also known as Pythagoras’s theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The theorem can be written as an equation relating the lengths of the sides a, b and c, often called the “Pythagorean equation”:[1]
where c represents the length of the hypotenuse and a and b the lengths of the triangle’s other two sides.
The example we got in Math class was a triangle where side “a” was 3 inches and side “b” was 4 inches and the hypotenuse was 5 inches. So: 3 squared (9) + 4 squared (16) = 5 squared (25).
(If you’re at all interested in reading more, and who wouldn’t be, here’s the Wikipedia link.)
The inside of the Lord’s temple was ninety feet long, thirty feet wide, and forty-five feet high.
1 Kings 6:2 (Contemporary English Version)
The hypotenuse of that space would have been about 94.87, as per the Calculate the Hypotenuse of a Right Triangle website.
And, something that is not at all germane to this conversation, but look what I found on the front sidewalk this morning. It’s a cicada. It didn’t seem very healthy, but it was early in the morning, and he might have just been fresh out of his little pupating shell. I’ve seen several round holes in the side yard, by the ferns. Maybe it’s cicada coming-out-party time.